tutorial outline

this tutorial deals with:

hardware implementation of single-rate dataflow models
example, Euclid's GCD algorithm:
- SDF graph analysis
- hardware implementation in Gezel
hardware pipelining:
- throughput enhancement
- warning about pipelining of SDF graphs with cycles
lab experience
- hardware implementations of dataflow models in Gezel and VHDL

single-rate SDF graph to hardware

hardware implementation assumption:

single-rate SDF graphs, all actors operate at the same clock frequency

three implementation rules:

all actors are implemented as combinational circuits
all communication queues are implemented as wires (without storage)
each initial token on a communication queue is replaced by a register

two definitions:

combinational path in the SDF graph: cycle-free path with no initial tokens on it
critical path in the SDF graph: combinational path that has maximum latency

maximum clock frequency for the circuit: reciprocal of latency through critical path

example: Euclid's GCD algorithm, SDF graph analysis

algorithm: at each step (a, b) is replaced by (|a-b|, min(a,b))

the pair converges to (GCD(a,b), GCD(a,b))

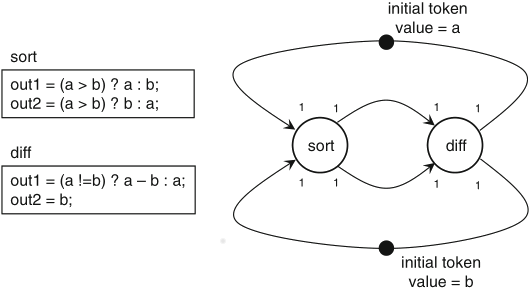
Schaumont, Figure 3.10 - Euclid’s greatest common divisor as
an SDF graph

Schaumont, Figure 3.10 - Euclid’s greatest common divisor as an SDF graph

PASS analysis:

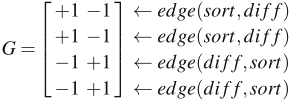
Schaumont, Equation 3.3 - topological matrix G of the SDF graph
for Euclid’s GCD algorithm

rank(G) = 1

Schaumont, Equation 3.4 - valid firing vector for matrix G

hardware implementation of Euclid's GCD algorithm

by the aforementioned three rules for a hardware implementation of the SDF model:

two combinational circuits implement the actors
a register is placed on each of the two connections from diff to sort

implementing the actors is a simple matter, by means of a few commonly used modules (multiplexers, comparators and a subtractor)

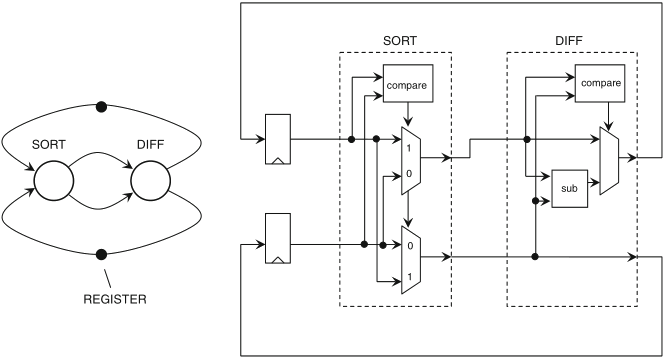
Schaumont, Figure 3.11 - Hardware implementation of Euclid’s
algorithm

Schaumont, Figure 3.11 - Hardware implementation of Euclid’s algorithm

hardware pipelining

example of throughput enhancement by pipelining:

digital filter to produce a weighted sum: x0⋅c2+x1⋅c1+x2⋅c0

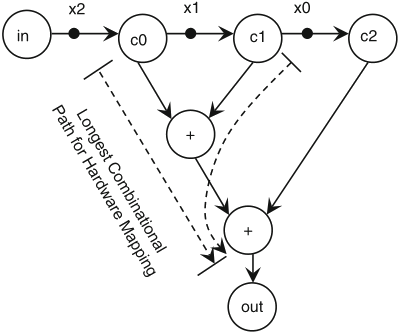
Schaumont, Figure 3.12 - SDF graph of a simple moving-average
application

Schaumont, Figure 3.12 - SDF graph of a simple moving-average application

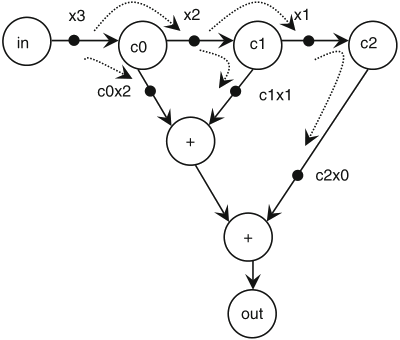
Schaumont, Figure 3.13 - Pipelining the moving-average filter
by inserting additional tokens (1)

Schaumont, Figure 3.13 - Pipelining the moving-average filter by inserting additional tokens (1)

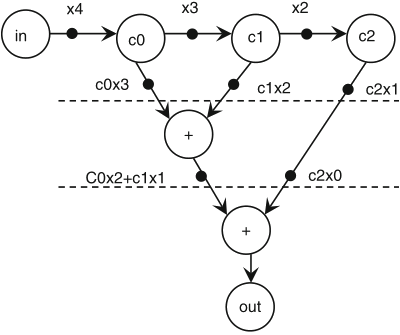
Schaumont, Figure 3.14 - Pipelining the moving-average filter
by inserting additional tokens (2)

Schaumont, Figure 3.14 - Pipelining the moving-average filter by inserting additional tokens (2)

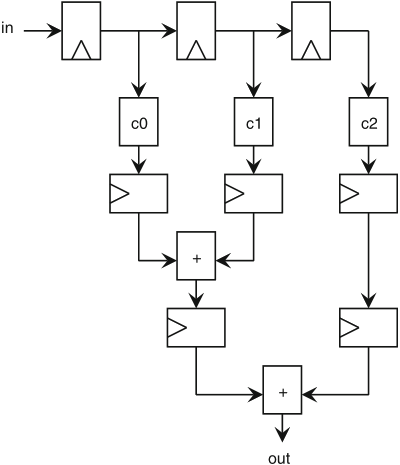
Schaumont, Figure 3.15 - Hardware implementation of the
moving-average filter

Schaumont, Figure 3.15 - Hardware implementation of the moving-average filter

remarks:

initial tokens here play the role of delay buffers in the definition of the pipelining transformation
the SDF graph is cycle-free... (see next)

pipelining in SDF graphs with loops

by introducing new tokens, pipelining may change the behaviour of an SDF graph

in particular, this may happen if additional tokens are introduced inside a loop, as this example shows:

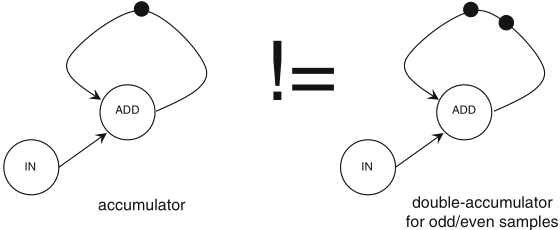
Schaumont, Figure 3.16 - Loops in SDF graphs cannot be pipelined

Schaumont, Figure 3.16 - Loops in SDF graphs cannot be pipelined

in order to apply pipelining without changing the functional behaviour of an SDF graph with cycles, the additional tokens should be placed outside of any loop in the graph

for instance, on the input or output lines

lab experience

the circuit depicted in figure 3.11 implements the computational core of Euclid's GCD algorithm, yet it does not contain elements apt to signal the start and the end of the computation nor to distinguish inputs and output; the aims of this experience are: to extend that circuit to this purpose, to describe it in Gezel, to translate it to VHDL, and to simulate its behaviour

extend the schematic of the circuit in figure 3.11 with three input signals and two output signals:
- a, b: the input data, 16-bit wide each
- start: 1-bit input, to signal the availability of the input data
- gcd: the 16-bit output result
- done: 1-bit output, to signal the end of the computation and the availability of the output result
and with additional elements (multiplexers, maybe a comparator) useful to the stated purpose
produce a Gezel description of the circuit from step 1
translate the Gezl description in VHDL by means of the fdlvhd program
launch Quartus 13.1 (Web edition), create a project EuclidGCD therein, and assign it the VHDL files produced in step 3
compile and simulate the VHDL model with different data input pairs

Dataflow network examples in Gezel and in VHDL

Tutorial 05 on Dedicated systems

Teacher: Giuseppe Scollo

University of Catania
Department of Mathematics and Computer Science
Graduate Course in Computer Science, 2016-17

Table of Contents