lecture topics

outline:

dataflow graphs
synchronous dataflow graphs (SDF)
PASS algorithm for SDF analysis
limitations of SDF graphs for control flow
SDF graph extensions for performance analysis
SDF graph transformations

dataflow graphs

high-level models for system design: block diagrams

aka filters and pipes architectures
each block (filter) processes an incoming data stream from its input channels and produces an outgoing data stream on its output channels
functional partitioning
uncommitted to hardware vs. software implementation

dataflow graphs: mathematical model of block diagrams

a model of computation (MoC)
widely used in signal processing
other related models: actor systems (Hewitt), Kahn networks, Petri nets, ...

example: block diagram of a 4-level pulse-amplitude modulation system (PAM-4)

see next

block diagram of a signal processing system

example: 4-level pulse-amplitude signal modulation (PAM-4)

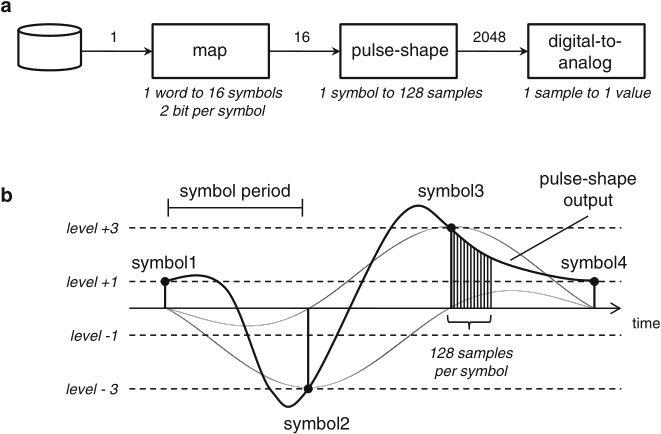
Schaumont, Figure 2.1 - (a) Pulse-amplitude modulation system.
(b) Operation of the pulse-shaping unit

Schaumont, Figure 2.1 - (a) Pulse-amplitude modulation system. (b) Operation of the pulse-shaping unit

usefulness of dataflow models for codesign

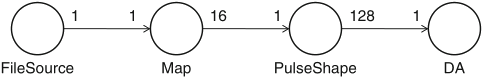
Schaumont, Figure 2.2 -
Data flow model for the pulse-amplitude modulation System

Schaumont, Figure 2.2 - Data flow model for the pulse-amplitude modulation system

a software model of the PAM-4 system is feasible, see for example the C program in Schaumont, Listing 2.1, where each block is represented as a function, yet:

the software model forces a sequential order of function execution
hardware implementations are feasible with parallel function execution, with their respective components operating in pipeline
a dataflow model allows both solutions

in the model in figure, functions are represented by actors linked through communication channels modeled as FIFO queues

every actor operates as an independent processing unit, with its inputs and outputs marked by the respective data consumption and production rates at every activation of the actor
strong features: dataflow graphs are a concurrent, distributed, modular MoC
thanks to their mathematical nature, dataflow graphs are amenable to analysis, allowing the designer to assess useful properties of an abstract architecture, e.g. deadlock freedom, well before its implementation

constituents of dataflow models

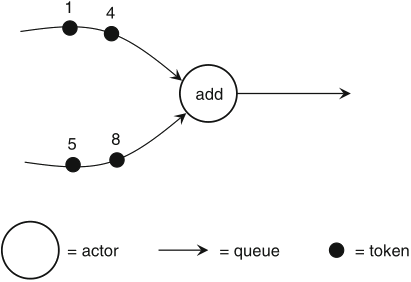
Schaumont, Figure 2.3 - Data flow model of an addition

Schaumont, Figure 2.3 - Data flow model of an addition

actors: iterative execution, each firing is subject to availability of data on all input channels
channels: unbounded FIFO queues
data: represented by values of tokens in the channels

Schaumont, Figure 2.4a - Result of first firing of the add actor

Schaumont, Figure 2.4b - Result of second firing of the add actor

Schaumont, Figure 2.4 - The result of two firings of the add actor, each resulting in a different marking

marking : state of a dataflow graph, consisting of an assignment of tokens to channels

Schaumont, Figure 2.7 - Example of a multi-rate data flow model

Schaumont, Figure 2.7 - Example of a multi-rate data flow model

synchronous dataflow (SDF) graphs

actors are functional processing units with no internal state

the only observable state information of a dataflow graph is its marking

in multirate dataflow graphs each actor may consume more than one token on each input channel and may produce more than one token on each output channel, at every firing

graphs with fixed production and consumption rates are said synchronous dataflow graphs (SDF)

SDF graphs cannot express data-dependent execution
however, mathematical analysis of their properties is easier
and, they are determinate (see figure)

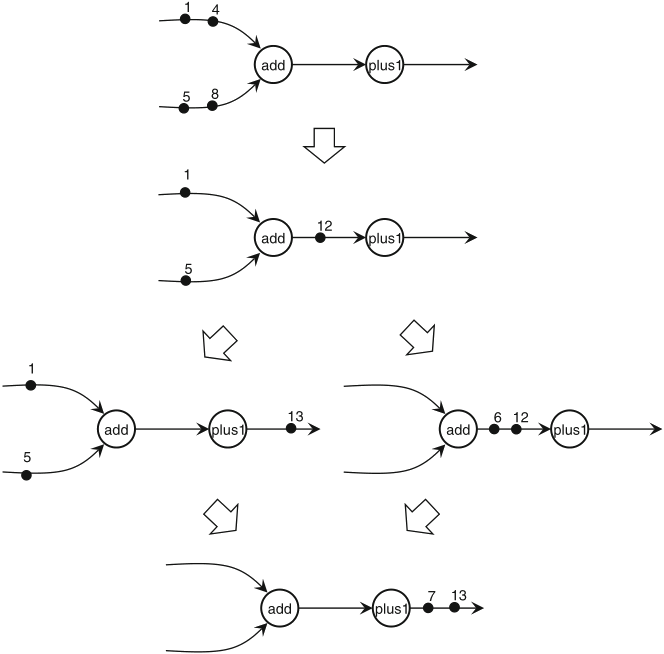
Schaumont, Figure 2.8 - SDF graphs are determinate

Schaumont, Figure 2.8 - SDF graphs are determinate

SDF graph analysis

desirable properties of an SDF graph:

unbounded execution
bounded buffers

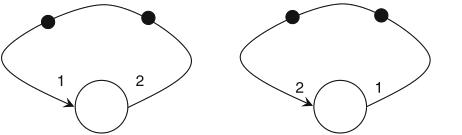
Schaumont, Figure 2.9 - Which SDF graph will deadlock, and
which is unstable?

Schaumont, Figure 2.9 - Which SDF graph will deadlock, and which is unstable?

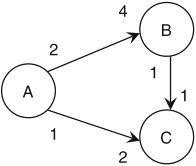
Schaumont, Figure 2.10 - Example SDF graph for PASS construction

Schaumont, Figure 2.10 - Example SDF graph for PASS construction

PASS: periodic admissible sequential schedule

sequential: firing of an actor at a time
admissible: deadlock-free + bounded buffers
periodicity of the state sequence → unbounded execution

PASS construction algorithm, if one exists (Lee):

create the topology matrix G of the SDF graph
verify rank of matrix = n. of actors minus one
determine a firing vector q such that Gq = 0
try round robin firing of each actor until count in firing vector

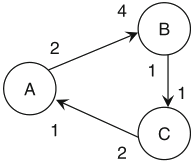
Schaumont, Figure 2.11 - A deadlocked graph

Schaumont, Figure 2.11 - A deadlocked graph

PASS example for the signal processing model

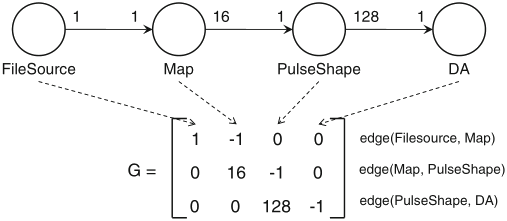
Schaumont, Figure 2.12 - Topology matrix for the PAM-4 system

Schaumont, Figure 2.12 - Topology matrix for the PAM-4 system

application of the method by Lee:

see figure
OK, the three rows of G are linearly independent
q^T = [1 1 16 2048]
the firing schedule described by q^T is a PASS, though it requires a 2048-position storage in the rightmost FIFO queue

a more economical solution is the schedule (1, 1, 16*(1, 128)), which only needs 128

limitations of data flow models for control flow

modeling control flow is not easy with SDF graphs...

a few problematic issues:

stopping and restarting
dynamic network topology
exception handling
run-time conditions, such as conditional execution
- a simple if-then-else is troublesome with SDF graphs
workarounds:
emulation in SDF with Fork-Sel actors
extension of SDF semantics to Boolean Data Flow (BDF)

Schaumont, Figure 2.13 - Emulating if-then-else conditions in SDF

Schaumont, Figure 2.13 - Emulating if-then-else conditions in SDF

Schaumont, Figure 2.14 - Implementing if-then-else using
Boolean Data Flow

Schaumont, Figure 2.14 - Implementing if-then-else using Boolean Data Flow

extensions of dataflow models for performance analysis

minimal extensions, preserving SDF semantics:

time: actor latency
space: bounded queues

useful for performance analysis and to evaluate performance-enhancing transformations

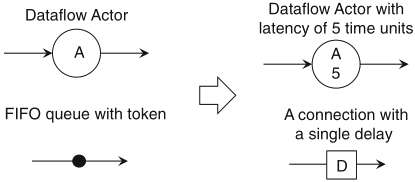
Schaumont, Figure 2.15 - Enhancing the SDF model with resources:
execution time for actors, delays for FIFO queues

Schaumont, Figure 2.15 - Enhancing the SDF model with resources: execution time for actors, delays for FIFO queues

Schaumont, Figure 2.16a

in the initial state, buffers always hold a token

Schaumont, Figure 2.16b

a buffer may hold a token for the duration of a single activation of the next actor

Schaumont, Figure 2.16c - Three data flow graphs

Schaumont, Figure 2.16 - Three data flow graphs

by adding buffers, pipelining may increase the throughput of an SDF graph

analysis of throughput limits

number and distribution of buffers in an SDF graph affect its throughput

loops also affect its latency and throughput; two concepts to see this:

loop bound: latency along a given loop divided by the number of buffers in that loop
iteration bound: highest loop bound in the graph

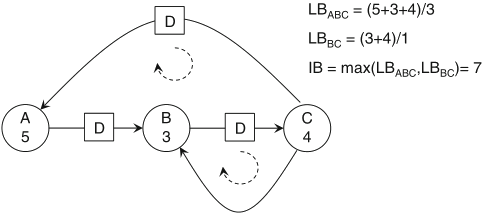
Schaumont, Figure 2.17 -
Calculating loop bound and iteration bound

Schaumont, Figure 2.17 - Calculating loop bound and iteration bound

the throughput of an SDF graph cannot be higher than (the reciprocal of) its iteration bound

linear graphs have an iteration bound, too (implicit feedback from output to input)

Schaumont, Figure 2.18 - Iteration bound for a linear graph

Schaumont, Figure 2.18 - Iteration bound for a linear graph

dataflow model transformations

functionality-preserving transformations aimed at improving the performance of SDF graphs

to increase the throughput and/or reduce the latency

four are most used:

multirate expansion : transforms a multirate SDF graph into a single-rate one
- useful because the other three are defined for single-rate SDF graphs
retiming : buffer redistribution over the graph edges
- to improve the throughput, no effect on latency nor on transient behaviour
pipelining : introduction of additional buffers to improve the iteration bound
- affects throughput and transient behaviour
unfolding : actor replication to increase the computational parallelism of the graph
- may affect the throughput, but not transient behaviour

multirate SDF graph expansion

transformation of a multirate SDF graph to single-rate, in 5 steps:

compute the actors' firing vector
replicate each actor as may times as indicated by its firing rate
replicate each I/O of each actor's replica into as many single-rate I/O's as indicated by its consumption/production rate
re-introduce the queues to connect all actors in the single-rate SDF
re-introduce the initial tokens, distributing them sequentially over the single-rate queues

Schaumont, Figure 2.19 - Multi-rate data flow-graph

Schaumont, Figure 2.19 - Multi-rate data flow-graph

Schaumont, Figure 2.20 - Multi-rate SDF graph expanded to
single-rate

Schaumont, Figure 2.20 - Multi-rate SDF graph expanded to single-rate

retiming

this transformation redistributes the buffers without changing their total number

treat the buffers as tokens, moving them along the queues according to the actors' firings, and evaluate the SDF graph performance in the different states of the succession to choose the one which exhibits the best performance

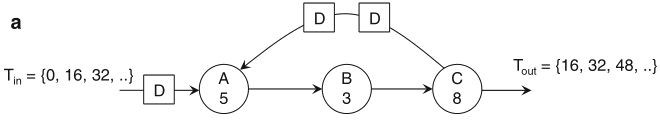
Schaumont, Figure 2.21a - Original graph

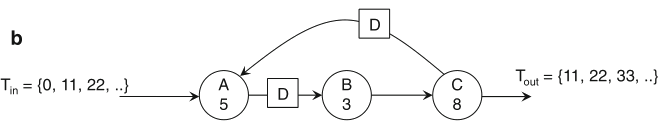
Schaumont, Figure 2.21b - Graph after first re-timing transformation

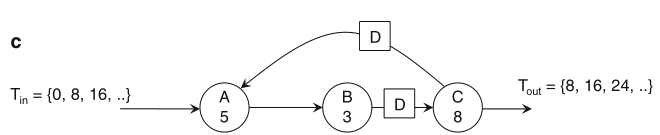
Schaumont, Figure 2.21c - Graph after second re-timing transformation

Schaumont, Figure 2.21 - Retiming: (a) Original Graph. (b) Graph after first re-timing transformation.
(c) Graph after second re-timing transformation

pipelining

pipelining = additional buffers + retiming

this transformation improves the throughput at the cost of an increased latency

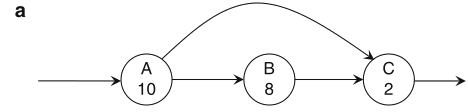
Schaumont, Figure 2.22a - Pipelining: Original graph

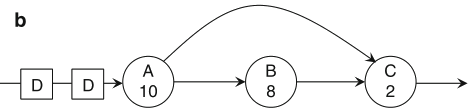
Schaumont, Figure 2.22b - Pipelining: Graph after adding
two pipeline stages

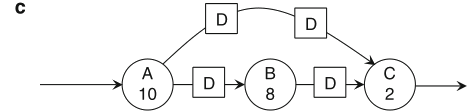
Schaumont, Figure 2.22c - Pipelining: Graph after retiming
the pipeline stages

Schaumont, Figure 2.22 - Pipelining: (a) Original graph. (b) Graph after adding two pipeline stages.
(c) Graph after retiming the pipeline stages

unfolding

replication of a given SDF graph into several copies in order to increase the parallelism of input stream processing

rules are partly similar to those of multirate expansion

the ν-unfolding of an SDF graph yields a graph with ν copies of each actor and of each edge

if edge AB connects actors A and B in the original graph, where it carries n buffers, then in the transformed graph, for i = 0..ν-1:

edge (AB)_i connects actor A_i with actor B_k where k = (i + n) mod ν
edge (AB)_i carries (i + n) / ν buffers (with ν-n edges without buffer if if n<ν)

Schaumont, Figure 2.23a - Unfolding: Original graph

Schaumont, Figure 2.23b - Unfolding: Graph after two-unfolding

Schaumont, Figure 2.23 - Unfolding: (a) Original graph.
(b) Graph after two-unfolding

Dataflow models, control flow

Lecture 03 on Dedicated systems

Teacher: Giuseppe Scollo

University of Catania
Department of Mathematics and Computer Science
Graduate Course in Computer Science, 2016-17

Table of Contents