funzioni e costanti speciali

cosa hanno di speciale?   sono di uso frequente nell'analisi degli algoritmi ...

• ... ed efficientemente approssimabili

eccone un quadro sintetico di valori tipici e approssimazioni (giustificate appresso)

costanti speciali : e ≈ 2.71828,  γ ≈ 0.57721,  φ = ( 1+√5 )/2 ≈ 1.61803

ln 2 ≈ 0.693147,  lg e = 1/ln 2 ≈ 1.44269

logaritmo naturale e serie armonica

• numeri armonici : approssimazione discreta dell'area sottesa dalla curva y = 1/x
  • H_N = 1 + 1/2 + 1/3 + ... + 1/N
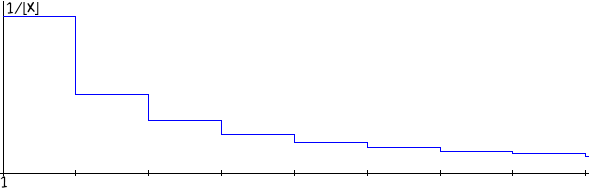
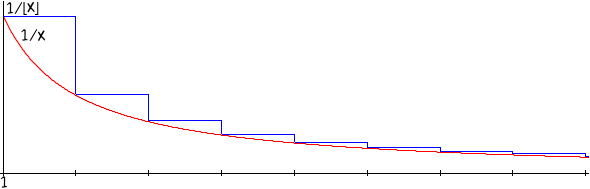
• la costante di Eulero γ misura l'area della differenza tra la funzione a gradino y = 1/_⌊x_⌋ e la funzione y = 1/x, per x ≥ 1, v. figura:

• tale significato di γ si coglie dall'approssimazione
  • H_N ≈ ln N + γ + 1/(12N)
• poiché ln N = ∫ ₁ ^N dx/x
• tale approssimazione permette un calcolo più efficiente di H_N, usando la funzione di libreria log, rispetto al calcolo diretto dalla definizione

serie di Fibonacci e sezione aurea

• numeri di Fibonacci : soluzione del noto problema dei conigli ...
  • definiti induttivamente: F_N = F_N-1 + F_N-2 , per N ≥ 2 , con F₀ = 0 e F₁ = 1
• l'apparentemente lenta velocità di crescita iniziale ...
  • 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
• ... non deve trarre in inganno:
  • il rapporto F_N+1/F_N fra due numeri di Fibonacci consecutivi, al crescere di N, tende al classico rapporto aureo φ = ( 1+√5 )/2 ≈ 1.61803
  • detto anche sezione aurea : sezione di un segmento in due parti tali che la minore stia alla maggiore come quest'ultima sta alla somma delle due
  • tale proporzione è frequente nell'arte ellenica (Fidia), e si riscontra anche nel corpo umano
• poiché il rapporto F_N+1/F_N tende a un valore costante > 1, la successione di Fibonacci acquista velocità di crescita esponenziale!
  • ciò è confermato dall'approssimazione asintotica :   F_N ≈ φ^N/√5

funzione fattoriale e formula di Stirling

definizione induttiva:   N! = (N-1)! N , per N > 0 , con 0! = 1

• la velocità di crescita di  N!  è superiore a quella di  k^N  per qualsiasi k
• N!  è il numero dei possibili ordinamenti di un insieme di N oggetti
• la formula di Stirling permette una rapida approssimazione asintotica del logaritmo binario del fattoriale:
  • lg N!  ≈  N lg N - N lg e + lg√2 π N
• dove il terzo addendo è asintoticamente trascurabile, il che giustifica l'approssimazione precedentemente proposta:
  • lg N!  ≈  N lg N - 1.44 N

stima asintotica e notazione O grande

che vuol dire esattamente che una funzione è un'approssimazione asintotica di un'altra?

la notazione O grande designa una limitazione asintotica della velocità di crescita:

def. :  g(N) è O(f(N)) se esistono costanti c e N₀ tali che g(N) < cf(N) per ogni N>N₀

utilità della notazione O grande:

• approssimazione in espressioni matematiche
  • ignorare i termini più piccoli
• approssimazione nella stima di prestazioni di algoritmi e programmi
  • ignorare le parti meno significative
• classificazione degli algoritmi
  • in termini di limiti superiori al tempo di calcolo

discendono direttamente dalla definizione molte proprietà della notazione O grande che permettono spesso di manipolarne le espressioni "come se la O non ci fosse", ad esempio:

• O(k) = O(1)   e   kO(f(N)) = O(kf(N)) = O(f(N)),   per ogni costante k,
• O(f(N)) + O(g(N)) = O(f(N)+g(N)),   O(f(N))O(g(N)) = O(f(N)g(N))

approssimazione funzionale

la limitazione asintotica espressa dalla notazione O grande non è sufficiente a caratterizzare la velocità di crescita

• ad esempio: kN è O(N²) ma ha crescita lineare, non quadratica

la notazione  ≈  (letta "all'incirca") designa l'approssimazione asintotica di una funzione con un'altra:

def. :   f(N) ≈ g(N) se  f(N) = g(N)+h(N)  e  h(N)/g(N) → 0 per N → ∞

per caratterizzare solo la velocità di crescita l'approssimazione asintotica chiede troppo... basta invece il seguente concetto

la notazione  ∝  (letta "proporzionale a") designa la proporzionalità asintotica di una funzione ad un'altra:

def. :   f(N) ∝ g(N) se esiste una costante c tale che   f(N) ≈ cg(N)