FSMD examples in Gezel and in VHDL

Tutorial 06 on Dedicated systems

Teacher: Giuseppe Scollo

University of Catania
Department of Mathematics and Computer Science
Graduate Course in Computer Science, 2019-20

tutorial outline

this tutorial deals with:

hardware implementation methods for FSMD models
FSMD design and implementation example
- design of a median computation datapath
- sequentialization by means of an FSMD
FSM description in VHDL
- description styles
- state encoding
- delay optimization
lab experience:
- design and FPGA implementation of a Collatz delay testbench

hardware implementation of FSMD models

hardware mapping of datapath expressions: same basic rules as with always blocks, however:

hardware datapath structure also depends on instruction schedule by FSM...
why?
consider the up-down counter example from the previous lecture:

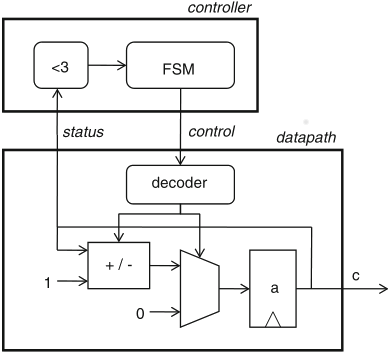
Schaumont, Figure 5.8 -
implementation of the up-down counter FSMD

Schaumont, Figure 5.8 - Implementation of the up-down counter FSMD

by the FSM model, different instructions will always execute in different clock cycles
instructions which are never concurrent may share operators' hardware
- such as the adder/subtractor in this case
a local decoder converts the instruction encoding into control signals for the datapath, to enable the proper execution path
a local decoder in the controller extracts datapath state information for the FSM conditions

FSMD design example: median computation

function specification: computation of the median in a list of five numbers

problem: design a stream-processing filter that produces a new output upon each new input

such filters find application in image processing, for noise reduction

for a fast algorithm, with no list sorting:

in a (2n +1)-element list, with pairwise distinct elements, the median has n smaller elements

dp median(in a1, a2, a3, a4, a5 : ns(32); out q1 : ns(32)) {
sig z1, z2, z3, z4, z5, z6, z7, z8, z9, z10 : ns(3);
sig s1, s2, s3, s4, s5 : ns(1);
always {
z1 = (a1 < a2);
z2 = (a1 < a3);
z3 = (a1 < a4);
z4 = (a1 < a5);
z5 = (a2 < a3);
z6 = (a2 < a4);
z7 = (a2 < a5);
z8 = (a3 < a4);
z9 = (a3 < a5);
z10 = (a4 < a5);
s1 = (( z1 + z2 + z3 + z4) == 2);
s2 = (((1-z1) + z5 + z6 + z7) == 2);
s3 = (((1-z2) + (1-z5) + z8 + z9) == 2);
s4 = (((1-z3) + (1-z6) + (1-z8) + z10) == 2);
q1 = s1 ? a1 : s2 ? a2 : s3 ? a3 : s4 ? a4 : a5;
}
}

Schaumont, Listing 5.19 - GEZEL Datapath of a median calculation of five numbers

the algorithm presented by this datapath also works when some elements are equal

the description is almost identical to that of a C function for the same algorithm
but with a substantial, practical difference:
sequential execution of assignments in C vs. parallel execution in the datapath
- where each output production requires just one clock-cycle!
provided all input values are simultaneously available ...
an FSMD may allow a big space saving, as we are going to see

datapath of a median computation datapath

the presented algorithm requires 192 I/O lines and 10 comparators

a stream processing filter may reduce these requirements to 64 I/O lines and 4 comparators

to this end the hardware stores the four data preceding the last one from the input stream and at every iteration with a new input element reuses the stored results of six comparisons from the previous three iterations

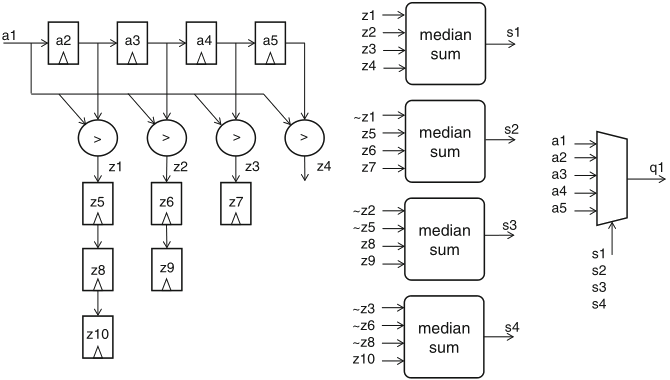
Schaumont, Figure 5.9 -
Median-calculation datapath for a stream of values

Schaumont, Figure 5.9 - Median-calculation datapath for a stream of values

dp median(in a1 : ns(32); out q1 : ns(32)) {
reg a2, a3, a4, a5 : ns(32);
sig z1, z2, z3, z4;
reg z5, z6, z7, z8, z9, z10 : ns(3);
sig s1, s2, s3, s4, s5 : ns(1);
always {
a2 = a1;
a3 = a2;
a4 = a3;
a5 = a4;
z1 = (a1 < a2);
z2 = (a1 < a3);
z3 = (a1 < a4);
z4 = (a1 < a5);
z5 = z1;
z6 = z2;
z7 = z3;
z8 = z5;
z9 = z6;
z10 = z8;
s1 = (( z1 + z2 + z3 + z4) == 2);
s2 = (((1-z1) + z5 + z6 + z7) == 2);
s3 = (((1-z2) + (1-z5) + z8 + z9) == 2);
s4 = (((1-z3) + (1-z6) + (1-z8) + z10) == 2);
q1 = s1 ? a1 : s2 ? a2 : s3 ? a3 : s4 ? a4 : a5;
}
}

sequentialization by means of an FSMD

the filter in fig 5.9 accepts a new input and produces a new output at every clock cycle

the number of computing components may be further reduced by distributing the computation over multiple clock cycles under a sequential schedule, so that a single comparator and a single module to compute s1, s2, s3, s4 are reused, at the cost of adding a few multiplexers and registers for the internal signals

the figure shows the schedule, the FSMD which implements this idea is in Schaumont Sect. 5.5.4, which also presents the testbench FSMD here reproduced aside the figure

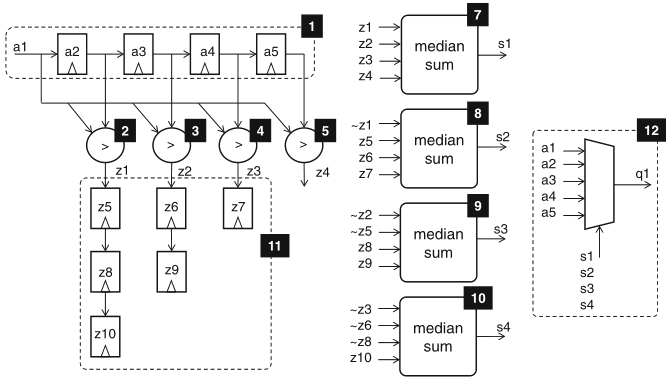
Schaumont, Figure 5.10 - Sequential schedule median-calculation
datapath for a stream of values

Schaumont, Figure 5.10 - Sequential schedule median-calculation datapath for a stream of values

dp t_median {
sig istr, ostr : ns(1);
sig a1_in, q1 : ns(32);
use median(istr, a1_in, ostr, q1);
reg r : ns(1);
reg c : ns(16);
always { r = ostr; }
sfg init { c = 0x1234; }
sfg sendin { a1_in = c;
c = (c[0] ˆ c[2] ˆ c[3] ˆ c[5]) # c[15:1];
istr = 1; }
sfg noin { a1_in = 0;
istr = 0; }
}
fsm ctl_t_median(t_median) {
initial s0;
state s1, s2;
@s0 (init, noin) -> s1;
@s1 (sendin) -> s2;
@s2 if (r) then (noin) -> s1;
else (noin) -> s2;
}

FSM description in VHDL

a simple example: memory controller

state transition diagram of a memory controller

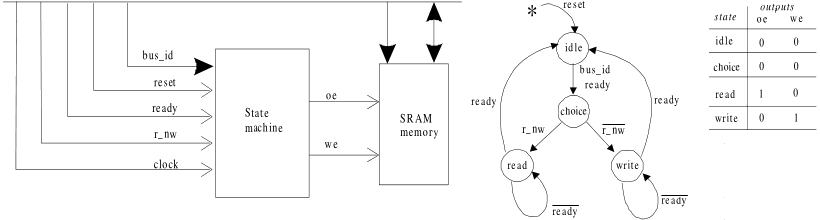
State transition diagram of a memory controller

general FSM hardware structure

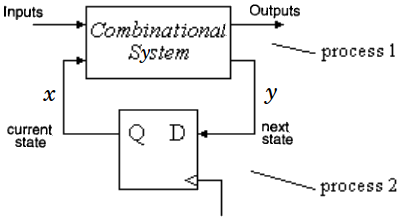
FSM hardware structure

in the VHDL description, states form an enumerated type

(see enclosed code):

two-process: most immediate way to reflect the scheme in the figure, one process is sensitive to the clock
- this is the translation style with fdlvhd
one-process: just one state signal, Moore FSM outputs may be described by concurrent assignments, outside the process
three-process: state transition and output functions described by distinct combinational processes

state encoding techniques

a binary encoding of the state enumerated type is needed to synthesize an HDL description of an FSM

automatically generated by the synthesis tool if not explicitly specified in the description

frequently used encodings:

sequential : compact, a set of n states is encoded in the set of binary representations of the natural numbers < n, with ⌈log₂n⌉ bits
one-hot : with as many bits as are the states, where only one bit is set to 1 in the encoding (bijection between states and bit positions in the encoding), automated synthesis often generates this encoding
ad-hoc to optimize the delay, see next page

explicit state encoding may be described in VHDL by defining the state type as a subtype of STD_LOGIC_VECTOR and by declaring the state encodings as constants of that type; for example, here are sequential and one-hot encodings of the states from the seen example:

subtype state is std_logic_vector(1 downto 0);
constant idle : state := "00";
constant choice : state := "01";
constant read : state := "10";
constant write : state := "11";

subtype state is std_logic_vector(3 downto 0);
constant idle : state := "0001";
constant choice : state := "0010";
constant read : state := "0100";
constant write : state := "1000";

if the encoding is not surjective, e.g. a one-hot encoding, the construct case stato is when ... must have the final clause when others ...

delay optimization

current-state dependent outputs (Moore FSM)

Current-state dependent outputs (Moore FSM)

the block diagram corresponds to the two-process and one-process descriptions in the enclosed code

a significant clock-to-output delay may result

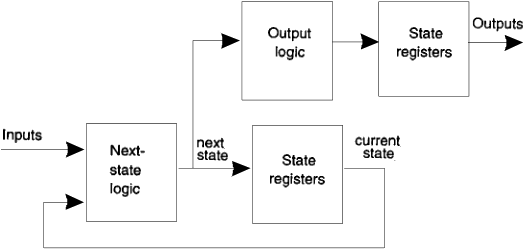
next-state dependent outputs

Next-state dependent outputs

this may be reduced to the flip-flop clock-to-q delay by computing outputs based on the next state and by placing registers before outputs

the three-process architecture in the enclosed code exemplifies this optimization

N.B. since processes are sequential, this optimization is also applicable to two-process and one-process architectures as well, by deferring outputs' updates until after state updates

reduction of clock-output delay

Reduction of clock-output delay

another optimization technique consists in encoding states so as to let outputs coincide with some of the (encoded) state bits

e.g. in the seen example:

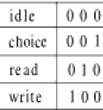
state three-bit encoding

lab experience

this experience has a twofold target

extension of the dataflow model out of the third lab experience for the delay computation of Collatz trajectories to an FSMD model that would include a pseudorandom generator feeding the datapath with initial values of trajectories, similar to the sendin instruction in the testbench example for the median computation filter, and that would alternate the output of the generated initial value with the output of the computed delay for the corresponding trajectory
- for the first target, translation to VHDL and simulation are required, the latter as a correctness check
implementation of the model on the DE1-SoC FPGA, with user control inputs to enable the alternating data output on a series of five 7-segment displays, in decimal representation

the I/O for the first target model consist of:

binary input start, to enable the start of a new trajectory, with output of the generated (16-bit) initial value
binary output done, to signal te end of computation of a trajectory delay
binary input dout, to enable the output of the computed delay, on the same port as of the initial value
display output of 16-bit numbers, multiplexed over the alternating output of initial value and delay as mentioned above

after the initial state where the generator is initialized, it is suggested to let the control FSM go through a sequence of four states:

wait for user control input start
output of the trajectory initial value, start up the delay computation, and wait for its completion
done output and wait for user control input dout
output of the delay value and back to state 1

for the second target, use can be made of the 7-segment display decoder from the two latest lab experiences, but this is to be fed with BCD representations of the 16-bit output decimal digits: five displays are needed to this purpose and package bcd, is available, that provides the BCD_encode function

use keys KEY0, KE1, KEY2 for inputs RST, start, dout, LED LEDR0 for output done, and CLOCK_50 for the clock

FSMD examples in Gezel and in VHDL

Tutorial 06 on Dedicated systems

Teacher: Giuseppe Scollo

University of Catania
Department of Mathematics and Computer Science
Graduate Course in Computer Science, 2019-20

Table of Contents

tutorial outline

hardware implementation of FSMD models

FSMD design example: median computation

datapath of a median computation datapath

sequentialization by means of an FSMD

FSM description in VHDL

state encoding techniques

delay optimization

lab experience

references

FSMD examples in Gezel and in VHDL

Tutorial 06 on Dedicated systems

Teacher: Giuseppe Scollo

University of Catania Department of Mathematics and Computer Science Graduate Course in Computer Science, 2019-20

University of Catania
Department of Mathematics and Computer Science
Graduate Course in Computer Science, 2019-20