lecture topics

outline:

overview of software implementation methods for dataflow models
implementation of FIFO queues in C
implementation of actors in C
example: SDF model of an FFT and its implementation
dynamic scheduling with cooperative multithreading
use of the QuickThreads library
implementation optimization with static schedule and inlining

software implementation methods for dataflow models

model elements to be mapped to software: actors, queues, firing rules

wide spectrum of implementation options:

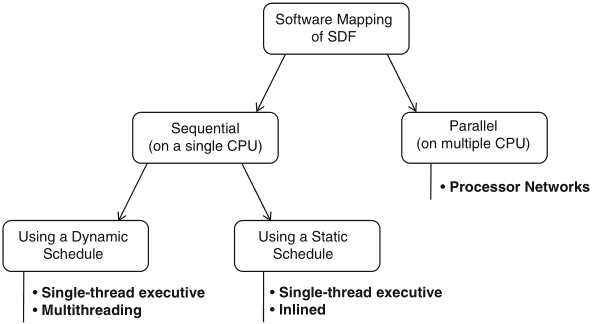
Schaumont, Figure 3.1 - overview of possible approaches to map
dataflow into software

Schaumont, Figure 3.1 - Overview of possible approaches to map dataflow into software

parallel implementation, optimization of distribution of actors over the processors:

computational load balancing
minimization of inter-processor communication

sequential implementation, options: scheduling, threading

static scheduling → further optimization opportunities

implementation of FIFO queues

FIFO queue, structure with:

two parameters: size, element data type
three operations: void put(element), element get(), int getsize()

it may be implemented as a circular array with two pointers to the access locations for the read and write operations, that are incremented mod N if the array size is N+1

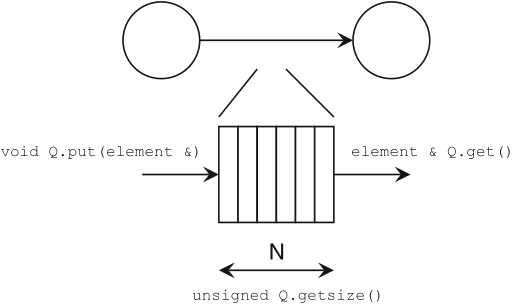
Schaumont, Figure 3.2 - A software queue

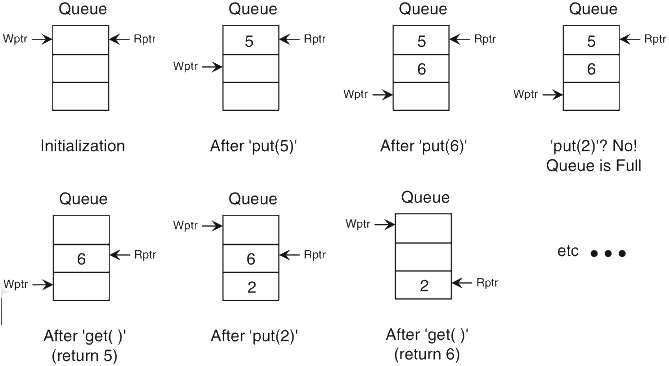
Schaumont, Figure 3.2 - A software queue

Schaumont, Figure 3.3 - Operation of the circular queue

Schaumont, Figure 3.3 - Operation of the circular queue

FIFO queue in C

#define MAXFIFO 8
typedef struct fifo {
  int data[MAXFIFO]; // token storage
  unsigned wptr; // write pointer
  unsigned rptr; // read pointer
} fifo_t;

void init_fifo(fifo_t *F) {
F->wptr = F->rptr = 0;
}

void put_fifo(fifo_t *F, int d) {
  if (((F->wptr + 1) % MAXFIFO) != F->rptr) {
    F->data[F->wptr] = d;
    F->wptr = (F->wptr + 1) % MAXFIFO;
  }
}

int get_fifo(fifo_t *F) {
  int r;
  if (F->rptr != F->wptr) {
    r = F->data[F->rptr];
    F->rptr = (F->rptr + 1) % MAXFIFO;
    return r;
  }
  return -1;
}

unsigned fifo_size(fifo_t *F) {
  if (F->wptr >= F->rptr)
    return F->wptr - F->rptr;
  else
    return MAXFIFO - (F->rptr - F->wptr);
}

int main() {
  fifo_t F1;
  init_fifo(&F1); // resets wptr, rptr;
  put_fifo(&F1, 5); // enter 5
  put_fifo(&F1, 6); // enter 6
  printf("%d %d\n", fifo_size(&F1), get_fifo(&F1));
  // prints: 2 5
  printf("%d\n", fifo_size(&F1)); // prints: 1
}

Schaumont, Listing 3.1 - FIFO object in C

implementation of actors

a C function, parameterized with a data structure to support I/O on the FIFO queues

actor I/O is subject to validity of its firing rule
- presence of the required number of tokens on each of its input queues
firing rule validity is checked by the actor itself upon every invocation

a first, elementary example of FSM with datapath (FSMD):

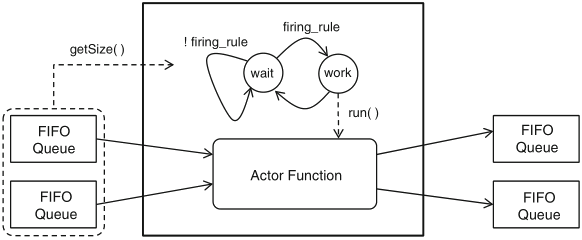
Schaumont, Figure 3.4 - Software implementation of the datafow actor

Schaumont, Figure 3.4 - Software implementation of the datafow actor

actor example in C

a data structure to support up to eight input queues and as many output queues:

#define MAXIO 8
typedef struct actorio {
fifo_t *in[MAXIO];
fifo_t *out[MAXIO];
} actorio_t;

an actor which reads two integer tokens and produces their sum and their difference:

void fft2(actorio_t *g) {
  int a, b;
  if (fifo_size(g->in[0]) >= 2) {
    a = get_fifo(g->in[0]);
    b = get_fifo(g->in[0]);
    put_fifo(g->out[0], a+b);
    put_fifo(g->out[0], a-b);
  }
}

with this arrangement, actors may be instantiated in the main program and invoked by dynamic scheduling

software implementation with a dynamic scheduler

a dynamic system scheduler instantiates and initializes actors and queues, then it invokes the actors–say, in a round robin fashion:

void main() {
  fifo_t q1, q2;
  actorio_t fft2_io = {{&q1}, {&q2}};
  ..
  init_fifo(&q1);
  init_fifo(&q2);
  ..
  while (1) {
    fft2_actor(&fft2_io);
    // .. call other actors
  }
}

Schaumont, Figura 3.5a - A graph which will simulate under a
single rate system schedule

Schaumont, Figure 3.5a - A graph which will simulate under a single rate system schedule

Schaumont, Figura 3.5b - A graph which will cause extra tokens
under a single rate schedule

Schaumont, Figure 3.5b - A graph which will cause extra tokens under a single rate schedule

system schedule

void main() {
  ..
  while (1) {
    src_actor(&src_io);
    snk_actor(&snk_io);
  }
}

a problem is apparent with the example in the second figure

solution 1: adjust system schedule

void main() {
  ..
  while (1) {
    src_actor(&src_io);
    snk_actor(&snk_io);
    snk_actor(&snk_io);
  }
}

solution 2: adjust actor snk code

void snk_actor(actorio_t *g) {
  int r1, r2;
  while ((fifo_size(g->in[0]) > 0)) {
    r1 = get_fifo(g->in[0]);
    ... // do processing
  }
}

example: SDF model of an FFT

the fast (discrete) Fourier transform is widely used in signal processing

twiddle factors (complex roots of unity): W_N^{^k} = W(k, N) = e^-j2π k/N

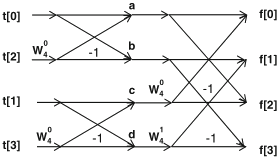
Schaumont, Figure 3.6a - Flow diagram for a four-point
Fast Fourier Transform

Schaumont, Figure 3.6a - Flow diagram for a four-point Fast Fourier Transform

a = t[0] + W(0,4) * t[2] = t[0] + t[2]
b = t[0] - W(0,4) * t[2] = t[0] - t[2]
c = t[1] + W(0,4) * t[3] = t[1] + t[3]
d = t[1] - W(0,4) * t[3] = t[1] - t[3]
f[0] = a + W(0,4) * c = a + c
f[1] = b + W(1,4) * d = b - j.d
f[2] = a - W(0,4) * c = a - c
f[3] = b - W(1,4) * d = b + j.d

an SDF model for the magnitude computation in the frequency domain:

Schaumont, Figure 3.7 - Synchronous dataflow diagram for a
four-point Fast Fourier Transform

Schaumont, Figure 3.7 - Synchronous dataflow diagram for a four-point Fast Fourier Transform

reorder : (t[0],t[1],t[2],t[3])→(t[0],t[2],t[1],t[3])
fft2 : the actor in example on p. 7
fft4mag : → 4-point transform magnitudes

software implementation of the FFT model

void reorder(actorio_t *g) {
  int v0, v1, v2, v3;
  while (fifo_size(g->in[0]) >= 4) {
    v0 = get_fifo(g->in[0]);
    v1 = get_fifo(g->in[0]);
    v2 = get_fifo(g->in[0]);
    v3 = get_fifo(g->in[0]);
    put_fifo(g->out[0], v0);
    put_fifo(g->out[0], v2);
    put_fifo(g->out[0], v1);
    put_fifo(g->out[0], v3);
  }
}

void fft2(actorio_t *g) {
  int a, b;
  while (fifo_size(g->in[0]) >= 2) {
    a = get_fifo(g->in[0]);
    b = get_fifo(g->in[0]);
    put_fifo(g->out[0], a+b);
    put_fifo(g->out[0], a-b);
  }
}

void fft4mag(actorio_t *g) {
  int a, b, c, d;
  while (fifo_size(g->in[0]) >= 4) {
    a = get_fifo(g->in[0]);
    b = get_fifo(g->in[0]);
    c = get_fifo(g->in[0]);
    d = get_fifo(g->in[0]);
    put_fifo(g->out[0], (a+c)*(a+c));
    put_fifo(g->out[0], b*b - d*d);
    put_fifo(g->out[0], (a-c)*(a-c));
    put_fifo(g->out[0], b*b - d*d);
  }
}

int main() {
  fifo_t q1, q2, q3, q4;
  actorio_t reorder_io = {{&q1}, {&q2}};
  actorio_t fft2_io = {{&q2}, {&q3}};
  actorio_t fft4_io = {{&q3}, {&q4}};

  init_fifo(&q1);
  init_fifo(&q2);
  init_fifo(&q3);
  init_fifo(&q4);

  // test vector fft([1 1 1 1])
  put_fifo(&q1, 1);
  put_fifo(&q1, 1);
  put_fifo(&q1, 1);
  put_fifo(&q1, 1);
  // test vector fft([1 1 1 0])
  put_fifo(&q1, 1);
  put_fifo(&q1, 1);
  put_fifo(&q1, 1);
  put_fifo(&q1, 0);

  while (1) {
    reorder(&reorder_io);
    fft2 (&fft2_io);
    fft4mag(&fft4_io);
  }
  return 0;
}

Schaumont, Listing 3.2 - 4-point FFT as an SDF system

dynamic scheduling with cooperative multithreading

with multithreading, dynamic scheduling is implemented by assigning each actor its own thread of execution

cooperative multithreading: actors release control, execution of each actor resumes from the point where that actor released control

often: round-robin scheduler + solution 2 seen earlier

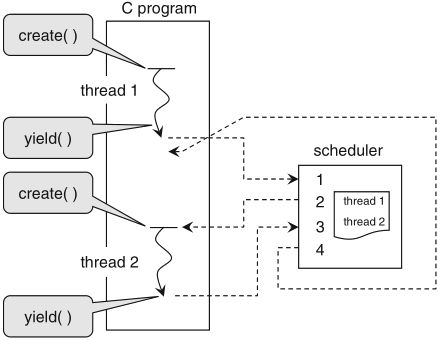
Schaumont, Figure 3.8 - Example of cooperative multi-threading

Schaumont, Figure 3.8 - Example of cooperative multi-threading

QuickThreads library functions:

stp_init()
stp_create(stp_userf_t *F, void *G)
stp_start()
stp_yield()
stp_abort()

implementation using the QuickThreads library

control release with stp_yield() keeps local variables throughout subsequent runs

#include "../qt/stp.h"
#include <stdio.h>
void hello(void *null) {
  int n = 3;
  while (n-- > 0) {
    printf("hello\n");
    stp_yield();
  }
}
void world(void *null) {
  int n = 5;
  while (n-- > 0) {
    printf("world\n");
    stp_yield();
  }
}
int main(int argc, char **argv) {
  stp_init();
  stp_create(hello, 0);
  stp_create(world, 0);
  stp_start();
  return 0;
}

application of this technique to the example developed in Listing 3.2 is very simple, e.g. for actor fft2:

void fft2(actorio_t *g) {
  int a, b;
  while (1) {
    while (fifo_size(g->in[0]) >= 2) {
      a = get_fifo(g->in[0]);
      b = get_fifo(g->in[0]);
      put_fifo(g->out[0], a+b);
      put_fifo(g->out[0], a-b);
    }
    stp_yield();
  }
}

int main() {
  fifo_t q1, q2;
  actorio_t fft2_io = {{&q1}, {&q2}};
  ...
  stp_create(fft2, &fft2_io); // create thread
  ...
  stp_start(); // run the schedule
}

optimization of implementation under static schedule

static scheduling allows optimization of a software implementation in three respects:

no need to check the firing rules in the actors' code
schedule optimization to minimize the storage requirements for the FIFO queues
code inlining:
- variables replace FIFO queues → space saving
- no function calls → time saving

example:

Schaumont, Figure 3.9 - System schedule for a multirate SDF graph

while(1) {
  // call A four times
  A(); A(); A(); A();
  // call B two times
  B(); B();
  // call C one time
  C();
}

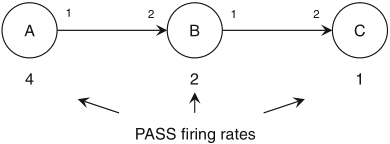
Schaumont, Figure 3.9 - System schedule for a multirate SDF graph

the static schedule in the figure is a PASS, yet it is not optimal for the minimization of the capacity of the queues: the firing sequence (A, A, B, A, A, B, C) is optimal

inlined implementation in C

optimized implementation of the FFT4 model on p. 9 with static schedule and inlining:

void dfsystem(int in0, in1, in2, in3, *out0, *out1, *out2, *out3) {
  int reorder_out0, reorder_out1, reorder_out2, reorder_out3;
  int fft2_0_out0, fft2_0_out1, fft2_1_out0, fft2_1_out1;
  int fft4mag_out0, fft4mag_out1, fft4mag_out2, fft4mag_out3;

  reorder_out0 = in0;
  reorder_out1 = in2;
  reorder_out2 = in1;
  reorder_out3 = in3;

  fft2_0_out0 = reorder_out0 + reorder_out1;
  fft2_0_out1 = reorder_out0 - reorder_out1;
  fft2_1_out0 = reorder_out2 + reorder_out3;
  fft2_1_out1 = reorder_out2 - reorder_out3;

  out0 = fft4mag_out0 = (fft2_0_out0 + fft2_1_out0) * (fft2_0_out0 + fft2_1_out0);
  out1 = fft4mag_out1 = fft2_0_out1*fft2_0_out1 - fft2_1_out1*fft2_1_out1;
  out2 = ftt4mag_out2 = (fft2_0_out0 - fft2_1_out0) * (fft2_0_out0 - fft2_1_out0);
  out3 = fft4mag_out3 = fft2_0_out1*fft2_0_out1 - fft2_1_out1*fft2_1_out1;
}

Schaumont, Listing 3.4 - Inlined data flow system for the four-point FFT

Software implementations of dataflow models

Lecture 04 on Dedicated systems

Teacher: Giuseppe Scollo

University of Catania
Department of Mathematics and Computer Science
Graduate Course in Computer Science, 2017-18

Indice