Docente: Giuseppe Scollo
Università di Catania, sede di Comiso (RG)
Facoltà di Scienze Matematiche, Fisiche e Naturali
Corso di Studi in Informatica applicata, AA 2008-9
come da lezione precedente, crittografia simmetrica e asimmetrica possono assolvere funzioni complementari per risolvere problemi di sicurezza informatica, ecco un caso tipico:
il problema della condivisione della chiave è circolare:
soluzione:
per proteggere la riservatezza della chiave trasmessa, e allo stesso tempo garantire l'autenticità del mittente, si adopera la doppia cifratura asimmetrica
proposto nel classico articolo del 1976, il protocollo di Diffie-Hellmann permette di stabilire una chiave segreta condivisa fra due partner che non condividono alcun segreto
la soluzione al problema è analoga a quella del seguente problema (da spy story):
il protocollo di Diffie-Hellmann presuppone che i partner A e B adoperino un opportuno grande numero primo p e un numero g di ordine (moltiplicativo) modulo p sufficientemente grande (N.B.: questa informazione, sebbene condivisa, non è segreta)
la simultanea garanzia di riservatezza e autenticità del mittente, fornita ad es. dalla doppia cifratura asimmetrica, trova applicazione anche nei sistemi di apposizione di firma elettronica
altri requisiti di sicurezza essenziali per la firma elettronica:
la doppia cifratura asimmetrica supporta la soddisfazione dei requisiti di protezione dell'integrità e di irripudiabilità della firma, per la segretezza della chiave di autenticazione
per garantire la non duplicabilità dei documenti, i sistemi di firma elettronica li possono corredare di informazione unica, ad es. temporale (timestamping)
la cifratura asimmetrica semplice può bastare quando non è in gioco la riservatezza
queste proprietà sono peraltro garantite anche da hash con chiave segreta (MAC)
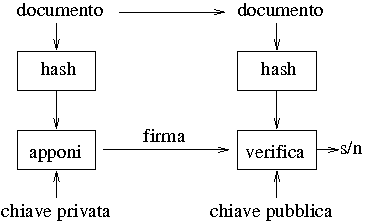
schema generico di firma digitale
la cifratura asimmetrica con chiave privata non è l'unico schema possibile di firma digitale
lo schema di firma Elgamal (Elgamal, 1984) lo dimostra
come per il protocollo di Diffie-Hellmann, la sua sicurezza dipende dalla difficoltà di calcolo del logaritmo discreto
schema essenziale: siano
≤ m < p
apposizione della firma:
≤ k < p, tale che
gcd(k, p-1) = 1
≡
m mod p-1
verifica :
deve valere l'equazione
yr rs
≡
gm mod p
la sicurezza dello schema Elgamal dipende da quella del problema del logaritmo discreto (DLP), ma non è equivalente ad essa
sono state sviluppate varianti dello schema Elgamal più sicure e più efficienti; alcune fra queste sono state tradotte in norme tecniche di uso pubblico:
per ulteriori informazioni su norme tecniche relative alla firma digitale, v. http://csrc.nist.gov/groups/ST/toolkit/digital_signatures.html
la verifica di autenticità, del mittente di un messaggio o autore di un testo, permessa dalla crittografia asimmetrica presuppone la certezza dell'associazione di una chiave pubblica all'identità, nota o conclamata, di una persona ...
problema: come acquisire tale certezza?
quando la persona non è nota, occorre una certificazione, della sua identità e/o di altre credenziali da essa conclamate, da parte di un terzo, degno di fiducia
in organizzazioni a struttura gerarchica, quale ad es. l'albero di un organigramma aziendale, la certificazione può basarsi su tale struttura, dove ciascun nodo dell'albero certifica la veridicità delle credenziali conclamate dai suoi nodi figli
quando la certificazione non può basarsi su una struttura gerarchica predefinita, si può fare ricorso ad un'autorità di certificazione che goda della fiducia delle parti interessate