Docente: Giuseppe Scollo
Università di Catania, sede di Comiso (RG)
Facoltà di Scienze Matematiche, Fisiche e Naturali
Corso di Studi in Informatica applicata, AA 2007-8
popolarità
degli alberi in informatica:
gli alberi sono inoltre presenti in una miriade di applicazioni: alberi genealogici, organigrammi, strutture di file system, strutture di libri, alberi sintattici, termini, ...
albero libero: grafo connesso privo di cicli
albero (radicato): albero con un vertice designato, detto radice
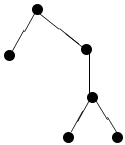
cammino:
sequenza di vertici distinti, con vertici successivi connessi da archi
ordinamento dei vertici:
terminologia: padre, figli, foglie, sottoalbero, ...
un albero è k-ario se ogni vertice ha al più al più k figli
un albero k-ario è completo se ogni vertice interno (cioè non foglia) ha k figli
un albero si dice ordinato se è definito un ordine (totale) sui figli di ciascun padre
l'altezza di un albero è la massima lunghezza (in n. di archi) dei cammini dalla radice
albero binario = albero k-ario, con k = 2
si rappresentano in tal modo alberi binari ordinati

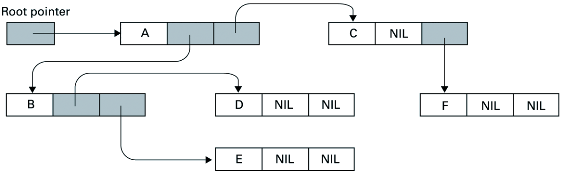
struct btree { Elem elem; btree *l, *r; };
typedef btree *btlink;
la rappresentazione vista degli alberi binari ben si presta ad operazioni su di essi per l'esecuzione delle quali si proceda dalla radice verso le foglie
la suddetta rappresentazione si generalizza facilmente ad alberi k-ari, dotando di k link la struttura di rappresentazione dei vertici, oltre all'eventuale link al vertice padre, quando ciò convenga
in tutti questi casi, si può anche scegliere una rappresentazione basata su array e indici invece di strutture e puntatori, poiché è prefissato un limite massimo al numero dei figli di qualsiasi vertice
una soluzione consiste nel rappresentare l'insieme (ordinato o meno) dei figli di un vertice interno mediante una lista
qui, però, un link punta al figlio più a sinistra, l'altro punta a un fratello del vertice
una foresta è un insieme di alberi che non condividono vertici
una foresta è ordinata se tale insieme è totalmente ordinato e gli alberi sono ordinati
gli alberi liberi sono grafi (non orientati) che soddisfano una proprietà caratteristica; questa può essere enunciata in vari modi: un grafo con N vertici è un albero libero se soddisfa una delle seguenti condizioni equivalenti:
un cammino in un grafo è una sequenza di vertici in cui vertici successivi sono connessi da un arco: il cammino è semplice se ogni vertice in esso occorre una sola volta
ogni cammino è semplice anche in un albero libero, caso particolare di foresta libera
un albero binario completo con N vertici interni ha N+1 foglie
un albero binario completo con N vertici interni ha 2N archi: N-1 fra vertici interni e N+1 con foglie
definizioni:
in un albero binario completo con N vertici interni, se I è la lunghezza del cammino interno ed E è la lunghezza del cammino esterno, allora E = I + 2N
l'altezza h di un albero binario completo
con N vertici interni soddisfa: ⌊lg N⌋+1 ≤ h ≤ N-1
la lunghezza del cammino interno, I, di un
albero binario completo con N vertici interni
soddisfa: N lg(N/4) <
I ≤
N(N-1)/2
⌊lg
N⌋,
di cui almeno due di livello ⌊lg
N⌋+1: moltiplicando e applicando l'ultima
proprietà dalla pagina precedente si ha>
(N+1)⌊lg
N⌋-2N
>
N lg(N/4)
(v. esercizio 7)
gli alberi bilanciati sono spesso utili al progetto di algoritmi ottimali
⇔
φ(u) ε2 φ(v)
⌊lg N⌋+1