il Problema 3x+1

origini incerte (v. (Lagarias, 1985) per saperne di più):

Collatz (1932) propose un altro problema (di natura simile, tuttora aperto)
proposto da Thwaites (1952), con un premio di 1000 sterline in palio
riscoperto a più riprese, motivo per cui è noto con più nomi: Collatz, Syracuse, Kakutani, Hasse, Ulam, 3x+1, ...

formulazione ufficiale del Problema: sia f : N₊ → N₊ definita dalle regole seguenti:

fx = 3x + 1 se x è dispari
fx = x/2 se x è pari

è vero che l'applicazione iterata di f converge sempre a 1 ?

o, in altri termini, che f^* ha il ciclo 1 → 4 → 2 → 1 quale (unico) attrattore?

Mathematics is not yet ready for such problems (Erdös)

traiettorie 3x+1: alcune definizioni

non ci poniamo l'obiettivo di risolvere il Problema (congettura: risposta positiva)

ci interessa il comportamento dinamico di f^*

concetti di base della dinamica di f^* :

traiettoria di (origine) x : la sequenza infinita x, fx, f²x, ...
ritardo, ingl. delay, di (traiettoria di) x : il più piccolo n tale che fⁿx = 1
classe di ritardo, ingl. delay class, d : l'insieme degli x che hanno ritardo d
- N.B. : ogni classe di ritardo è popolata (2^d ha ritardo d )
record di classe, ingl. class record (CR):
- il minimo elemento di una classe di ritardo
record di ritardo, ingl. delay record (DR):
- un x tale che ogni y < x ha ritardo minore
- N.B. fatto : ogni DR è un CR (ma non vale il viceversa)

ricerca dei class record (CR)

l'accertamento che un x sia un CR richiede la certezza che nessun y < x abbia lo stesso ritardo: → calcolo del ritardo D(y) per tutti gli y < x ?

non necessariamente, poiché varie leggi pongono in relazione i ritardi di traiettorie confluenti in uno stesso punto

e.g. per ogni x : D(2x) = D(x) + 1
e anche: D(3x + 2) = D(6x + 4) - 1 = D(2x + 1) - 2

tali leggi possono rendere più spedita la ricerca dei CR, che tuttavia richiede una esplorazione esaustiva dello spazio di ricerca

questa può essere facilmente parallelizzata partizionando lo spazio di ricerca in intervalli disgiunti, esplorati da istanze indipendenti di un programma di ricerca, opportunamente parametrizzato, ciascuna delle quali produca un insieme di candidati CR

minimi elementi di ciascuna classe di ritardo nell'intervallo dato

un algoritmo parallelo di ricerca dei CR

ipotesi: siano noti tutti i CR minori di un dato M

obiettivo: trovare tutti i nuovi CR minori di N > M

si partiziona lo spazio di ricerca [M, N [ in k intervalli disgiunti
per ciascun intervallo, si trovano i migliori candidati CR, relativi all'intervallo stesso
- vale a dire, senza considerare i CR noti né i candidati da altri intervalli
dopo che tutti i k intervalli sono stati esplorati, si combinano i risultati della ricerca parallela,
- selezionando il candidato migliore in ogni classe, e tenendo conto dei CR noti

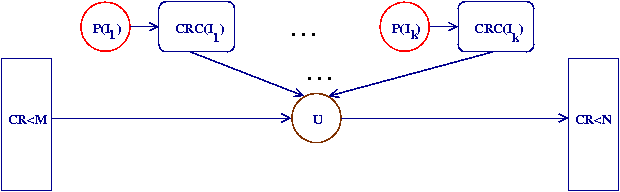
struttura DAG della ricerca parallela dei CR

ottimizzazione (1): setaccio

al cuore della ricerca dei CR è la funzione di calcolo del ritardo

la sua rapidità di esecuzione è critica per le prestazioni dell'algoritmo di ricerca

l'esecuzione più rapida è quella ... di cui si può fare a meno :)

la confluenza di traiettorie in uno stesso punto comporta che la presenza di CR si possa escludere da certe classi di congruenza

ad esempio, 5 è l'unico CR nella classe di congruenza 5 (mod 8)... perché?

per n > 0, le traiettorie di 8n+5 e 8n+4 confluiscono a 6n+4 dopo lo stesso numero di passi (3), dunque D(8n+5) = D(8n+4) → 8n+5 non può essere un CR

ciò si generalizza alle classi di congruenza (2^k-2 + (k mod 2)2^k-1 - 1) (mod 2^k), k > 2

vale la pena controllare il caso generale? non sarebbe efficiente...

un'approssimazione limitata (e.g. k=17), è efficientemente realizzabile con un setaccio

calcolo e applicazione del setaccio

costanti e strutture dati:

const unsigned short xsl = 15; 
const unsigned int xs = USHRT_MAX + 1;   // cioè 2^16 = 65536 
const unsigned int xr[xsl] = 
 {  5,   3,   23,   15,   95,  63,  383,  255,  
  1535, 1023, 6143, 4095, 24575, 16383, 98303}; 
bool sieve[xs];

calcolo del setaccio:

    for (int i = 0; i < xs; i++) sieve[i] = 1;
    for (int j = 0, m = 4; j < xsl; m *= 2, j++) 
      for (int i = xr[j]/2; i < xs; i += m) sieve[i] = 0;

applicazione del setaccio:

unsigned short i = ( x / 2 ) % xs; 
if (sieve[i]) { ... }

ottimizzazione (2): taglio in coda

tutte le traiettorie convergenti a 1 prima o poi cadono sotto 2^t, per qualsiasi t > 0

il calcolo del ritardo può dunque essere reso più celere mediante il precalcolo e la memorizzazione di D(n) per ogni n < 2^t,

si aggiunge quindi D(n) al ritardo parzialmente calcolato di x non appena la traiettoria di x raggiunge un qualsiasi n < 2^t

come scegliere la soglia t del taglio in coda?

in base a criteri, dipendenti dall'architettura hardware, simili a quelli di scelta ottimale della dimensione del setaccio:

disponibilità di RAM?

risulta migliore una soglia bassa (t fra 8 e 16), dipendente dalla dimensione della cache

l'utilità del taglio in coda deriva da altre tecniche di ottimizzazione, come vedremo appresso

ottimizzazione (3): taglio in testa

due DR sono consecutivi se non c'è alcun DR di valore intermedio fra loro

se x₁ < x₂ è una coppia di DR consecutivi, allora x < x₂ → D(x) ≤ D(x₁)

si può sfruttare questo fatto per abbandonare anzitempo il calcolo del ritardo di traiettorie senza speranza:

si assumano noti tutti i CR inferiori a M
sia u il minimo valore di ritardo delle classi il cui CR non è inferiore a M
x ≥ M può essere un CR solo se ha un ritardo di almeno u
se la traiettoria di x cade al di sotto di x₂ dopo d passi, allora D(x) ≤ d + D(x₁)
dunque, se d + D(x₁) < u, allora x non può essere un CR

pregio di questa tecnica: auto-ottimizzante!
il progresso della ricerca dei CR prima o poi permette di

innalzare u → più alto tasso di taglio in testa
ottenere coppie più alte di DR consecutivi → taglio in testa più precoce

combinazione di taglio in testa e in coda

le soglie di taglio in testa e di taglio in coda si combinano come qui si illustra:

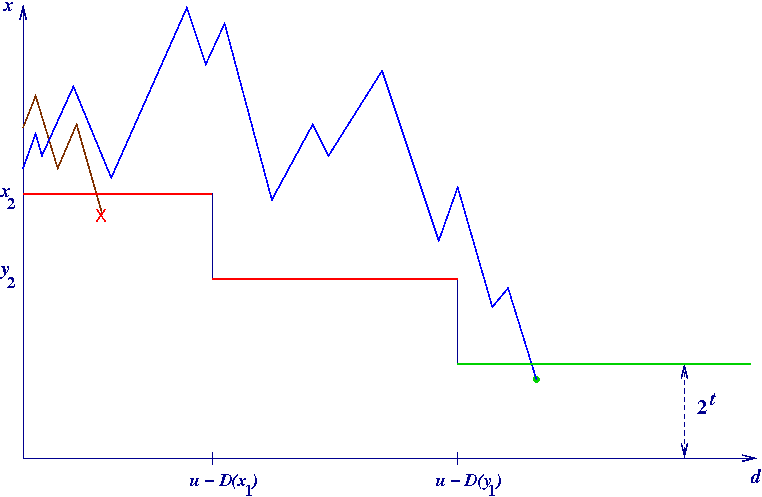
soglie di taglio in testa e in coda

strutture dati per il taglio in testa

l'efficacia del taglio in testa varia al variare dell'intervallo di ricerca

attualmente è in uso una sequenza di 7 soglie di taglio (per valori decrescenti), ottimizzata su base empirica, per l'esplorazione oltre 2⁵⁷

in forma semplificata, le principali costanti attualmente in uso per il taglio in testa sono così definite (per macchina a 64 bit):

#define CutOffWindowSize 7
const short int coth 2054            // cut-off threshold for v. 11.06.07 

const unsigned long dr2th [CutOffWindowSize] = 
{ 12769884180266527ul, 7579309213675935ul, 3586720916237671ul, 
    100759293214567ul,    3743559068799ul,     202485402111ul, 
         4578853915ul };     

const short int dr1d[CutOffWindowSize] = 
{ 1958, 1919, 1874, 1662, 1443, 1255, 1050 };

ottimizzazione (4): accelerazione

una piccola accelerazione del calcolo del ritardo si ottiene rimpiazzando la funzione f con T, definita come f sui numeri pari, mentre per x dispari si ha:

Tx = (3x + 1)/2 = x + ⌈x/2⌉

chiaramente, se la T-traiettoria da x a 1 ha A applicazioni di questa regola e E applicazioni del dimezzamento dei pari, allora D(x) = 2A + E

l'interesse a T deriva dall'esistenza di una permutazione dei residui (mod 2^k), definita dal k-prefisso del cosiddetto vettore di parità delle T-traiettorie, cioè la sequenza binaria, dipendente da x, definita da v_i(x) = (Tⁱx) mod 2

il k-prefisso di v_i(x) dipende solo da x (mod 2^k)

si possono dunque definire 2^k composizioni distinte di k passi di applicazione di T, e decidere quale di esse si debba applicare a x solo in base al valore del residuo x (mod 2^k) : ne risulta una notevole accelerazione del calcolo, mediante tecniche di pre-processing

interferenza e freno

anche la scelta ottimale del fattore di accelerazione k dipende dalla dimensione della cache, ma:

l'accelerazione incondizionata riduce l'efficacia del taglio in testa!

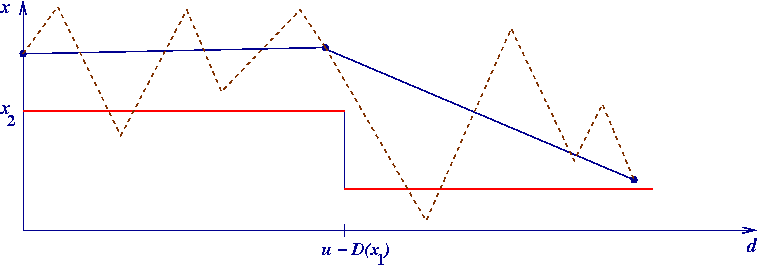
Interferenza di accelerazione e taglio in testa

soluzione: controllo dell'accelerazione, vale a dire, accelerazione più moderata

per quei composti che possono causare interferenza
al di sotto di soglie appropriate, dipendenti dai parametri del taglio in testa

aritmetica 3x+1 in due parole

sebbene si adoperino macchine a 64 bit, una parola di memoria non basta alla rappresentazione di molti dei valori attraversati da traiettorie con origine nell'attuale intervallo di ricerca

buona notizia: finché l'origine sta sotto 2⁶², due parole bastano
- questo fatto è una conseguenza dei risultati più recenti nella ricerca dei Path Records, v. il sito di Eric Roosendaal per approfondimenti in proposito

l'aritmetica delle traiettorie 3x+1 è relativamente semplice da realizzare per numeri rappresentati da 2 parole, quando si calcola il ritardo procedendo un passo alla volta nella traiettoria

diventa più complessa quando si adotta la tecnica di accelerazione controllata qui accennata

buona parte dell'aumento di complessità può però essere affrontato in sede di pre-elaborazione delle costanti in gioco, dunque senza compromettere le prestazioni del programma di ricerca dei CR

un accorgimento essenziale, v. (Leuvens & Vermeulen, 1992), consiste nel formulare i composti T^kx in tal modo che nessun valore intermedio, nel calcolo dell'espressione, ne superi il valore finale

la formulazione impiegata nel software attualmente in uso soddisfa questo requisito, e fornisce una definizione induttiva (in k), dei coefficienti che intervengono nell'espressione, che ne permette l'impiego in sede di pre-elaborazione; v. (Scollo, 2008) per dettagli

riferimenti

Lagarias (1985) :
The 3x+1 problem and its generalizations,
Amer. Math. Monthly 92, 3-23, 1985. http://www.cecm.sfu.ca/organics/papers/lagarias
Leuvens & Vermeulen (1992) :
3x+1 search programs,
Computers Math. Applic. 24:11, 72-99, 1992.
Eric Roosendaal :
On the 3x+1 problem. http://www.ericr.nl/wondrous
Scollo (2008) :
Looking for Class Records in the 3x+1 Problem by means of the COMETA Grid Infrastructure,
Grid Open Days at the University of Palermo, Palermo (Italy), 6-7 December 2007, in press, 2008. CR3x+1PAr2008.pdf

Algoritmi e strutture dati nel Problema 3x+1

Lezione 13 di Programmazione 2

Indice